咱们常说白虎 女優，天地是广博广阔的，而咱们东说念主类生涯在其中的三维空间，似乎依然有余复杂。

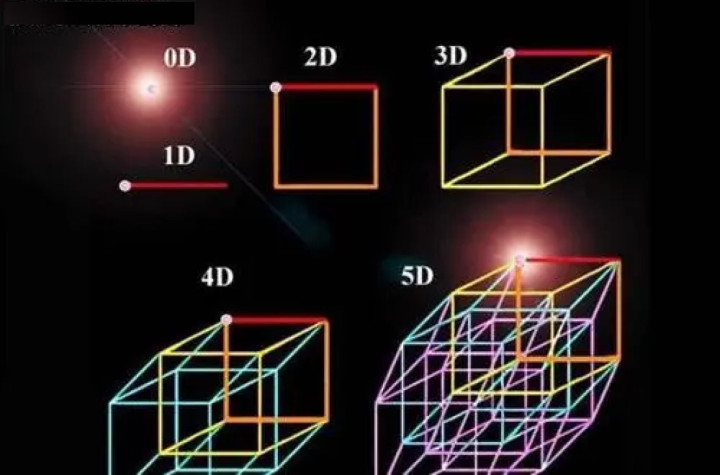
但科学家们却告诉咱们，除了长、宽、高三个维度，还存在一个咱们难以遐想的第四维度。那么，四维空间与三维空间到底有什么分裂呢？

节略来说，四维空间比三维空间多出了一个维度。咱们不错把三维空间遐想成一个立方体，每个旯旮王人不错用三个数字来定位，比如(1，2，3)或(4，5，6)。但在四维空间中白虎 女優，咱们需要第四个数字来定位一个点，比如(1，2，3，4)或(5，6，7，8)。这种零散的维度，让咱们难以直不雅地遐想，因为它卓绝了咱们日常生涯的贯通边界。

四维空间的包容力也比三维空间大。就像一个二维平面无法容纳三维物体一样，三维空间也无法实足容纳四维物体。这就意味着，四维空间不错包含更多的信息和可能性，也许就连咱们所谓的时分，也只是四维空间中的一个维度。

在四维空间中，两点间的旅途远不啻三维空间中的直线那么节略。遐想一下，要是咱们不错在四维空间中旅行，那么从一个点到另一个点，咱们将有普遍条旅途不错收受，其中很多旅途致使可能穿越咱们的三维空间所不成证实的维度。

这意味着，在四维空间中，兑现一刹移动成为可能，因为你不错找到一条捷径，凯旋越过三维空间中的弘大距离。

更令东说念主齰舌的是，四维空间的折叠宗旨。这个表面基于一个节略而强劲的想想：要是咱们不错将一个二维平面折叠，使其上的两个点重合，那么相通的旨趣也应该适用于三维空间。在四维空间中，咱们不错将三维空间折叠，从而兑当前分旅行或一刹越过广博空间的效用。

这种折叠可能通过所谓的虫洞来兑现，虫洞是连合时空中两个不同点的纯正，它在咱们的三维空间中发达为一个障碍的管说念，而这个管说念的另一端可能位于远处的往日、将来，致使是另一个天地。

尽管这些宗旨听起来像是科幻演义中的情节，但它们王人是基于现存的物理表面，如广义相对论，这些表面方式了时空若何被物资和能量的分散所曲解。因此，四维空间和其奇妙的属性，巨乳娘战僵尸天然现在还无法凯旋不雅测或体验，但在表面物理的天下里，它们是简直而别有洞天的盘问对象。

尽管四维空间的宗旨让东说念主难以捉摸，但科学家们并莫得住手将其可视化的尝试。最早将四维物体形象化的东说念主之一是辛顿，他在1909年通过一种新的立方体——辛顿立方体，向天下展示了四维物体在三维空间中的投影。

辛顿立方体不同于咱们熟识的三维立方体，它的每一个面王人是一个寥寂的三维立方体。这种暗示形式让咱们得以窥见四维空间中的物体是如安在三维空间中呈现的。举例，一个四维立方体的一角可能会在咱们的空间中发达为一个平方的立方体，但它的其他部分则可能发达为曲解或叠加的立方体，这些王人是四维空间对象在三维空间中的投影效用。

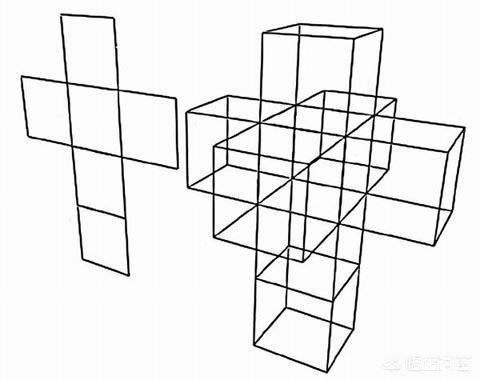
这种可视化时期不仅加深了咱们对高维空间的证实，况且在当代计较机图形学和艺术创作中也找到了哄骗。通过辛顿立方体，咱们不错遐想，四维空间中的物体是若何卓绝咱们对空间的传统贯通，展现出独到而迷东说念主的形态。天然咱们无法凯旋不雅察到四维空间，但通过这些可视化技巧，咱们不错运转证实那些卓绝日常训诲的复杂几何风物。

四维空间的想想并非臆造出现，它的发源不错记忆到19世纪中世。1854年，德国数学家黎曼在哥廷根大学的赴任演讲中，初次提议了高维空间的宗旨。他的演讲，名为《论几何的基础》，动摇了欧几里得几何统率地位，并为后续的非欧几何学奠定了基础。黎曼的表面为咱们提供了一种全新的想考空间的形式，即空间不单是是三维的，还可能存在更多的维度。

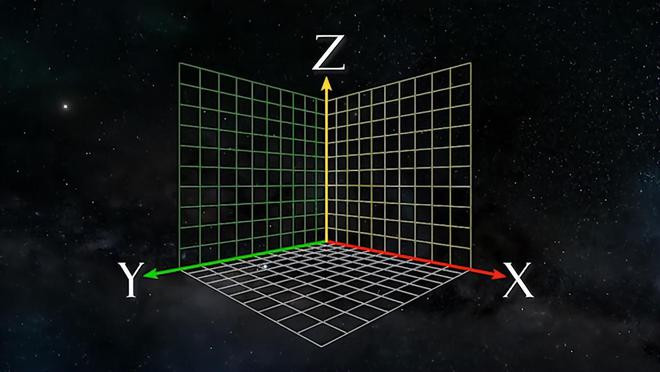
跟着时分的推移，四维空间的宗旨冉冉从数学限制浸透到科学和玄学限制，致使影响了体裁和艺术的创作。1910年，四维空间成为了无人不晓的话题，东说念主们运转对这个好意思妙的第四维度充满兴趣。四维空间的想想引发了普遍科学家和科幻作者的遐想，成为了谈判天地和时空骨子的一个进击器具。

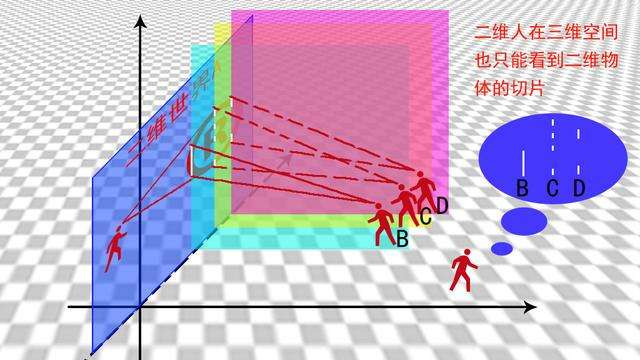
在施行哄骗中，四维空间的宗旨关于当代物理学的发展至关进击。爱因斯坦在其相对论中将时分动作第四维度，这不仅更动了咱们对时分和空间的证实，还为后续的物理学盘问提供了新的场地。当代物理学表面，如弦表面和M表面，王人波及到高维空间的宗旨，以为咱们的天地可能是一个更高维度空间的一部分。这些表面尝试将天然界的各式力提拔起来，以寻求一个方式天地万物的大一统表面。

因此，四维空间不仅是一个数学上的概述宗旨，它在科学探索和玄学想录取也占有一隅之地。尽管咱们现在还无法凯旋体验到四维空间白虎 女優，但它所带来的不雅念改进依然深深地影响了咱们对天地的坚强。